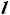 ),
корневой и концевой хорды (
),
корневой и концевой хорды (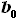 и
и 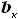 ), а для крыла с наплывом - также
хорды, соответствующей концу наплыва (
), а для крыла с наплывом - также
хорды, соответствующей концу наплыва (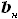 ) и размаха наплыва (
) и размаха наплыва (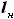 ),
),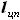 или
или 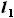 ) и размаха части крыла, имеющей
топливные баки (
) и размаха части крыла, имеющей
топливные баки (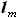 ),
), ,
, .
.
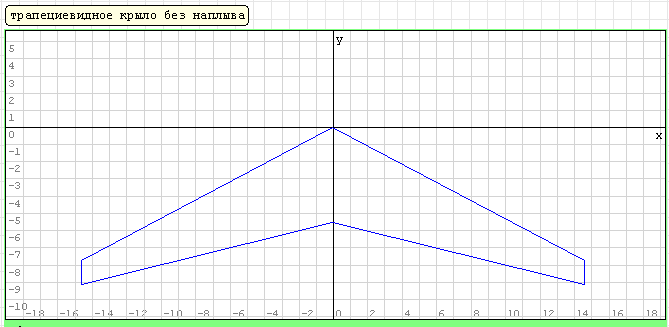

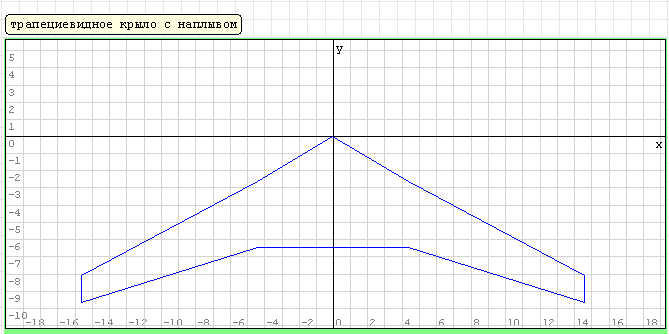
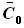 у корня до
у корня до 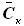 на конце. V-образность
крыла мала и ей можно пренебречь.
на конце. V-образность
крыла мала и ей можно пренебречь.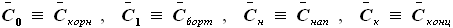 ,
, 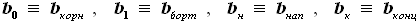 и т.д.
и т.д.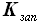 .
Коэффициент учитывает что часть объёма занята силовыми элементами
кессона, а также пенополиуретановой губкой для защиты от взрыва при
простреле. Значение
.
Коэффициент учитывает что часть объёма занята силовыми элементами
кессона, а также пенополиуретановой губкой для защиты от взрыва при
простреле. Значение 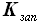 принимаем константой (значение в диапазоне
0,7..0,85), таким образом, остаётся найти объём кессона.
принимаем константой (значение в диапазоне
0,7..0,85), таким образом, остаётся найти объём кессона.
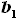 ), а с другой - концевой (хорда
), а с другой - концевой (хорда
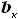 ). А у крыла с наплывом консоль состоит из двух фрагментов: первый
ограничен бортовой нервюрой (
). А у крыла с наплывом консоль состоит из двух фрагментов: первый
ограничен бортовой нервюрой (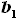 ) и хордой в месте окончания наплыва
(
) и хордой в месте окончания наплыва
(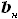 ), а второй - хордой
), а второй - хордой 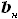 и концевой нервюрой (
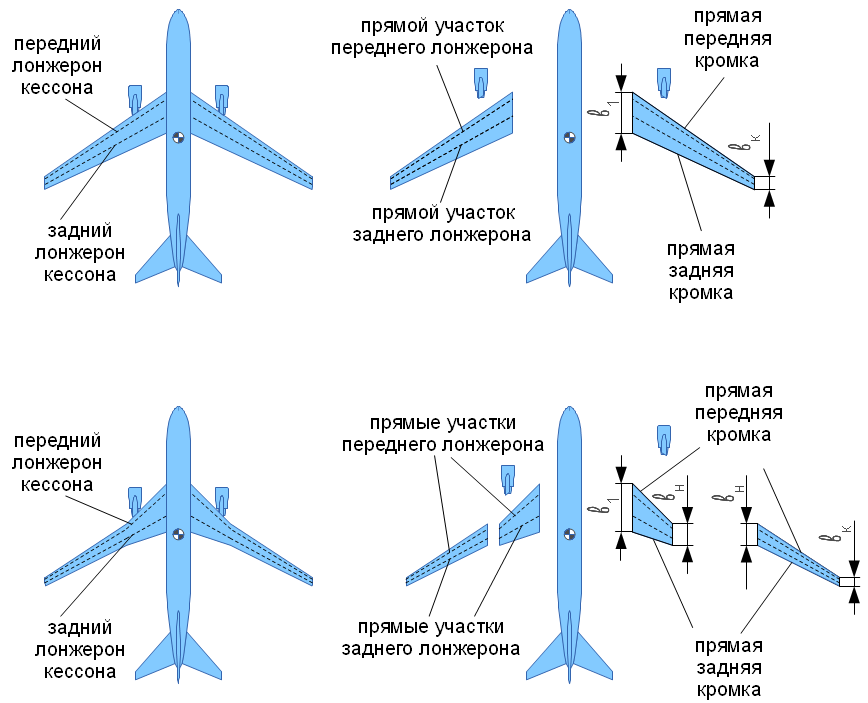
и концевой нервюрой (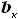 ).
).
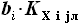 , где
, где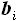 - длина i-ой хорды,
- длина i-ой хорды,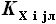 - коэффициент, имеющий значение в диапазоне 0..1, определяющий
отношение расстояния от носка i-ой хорды до точки её пересечения с j-м
лонжероном к длине i-ой хорды
- коэффициент, имеющий значение в диапазоне 0..1, определяющий
отношение расстояния от носка i-ой хорды до точки её пересечения с j-м
лонжероном к длине i-ой хорды 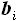 .
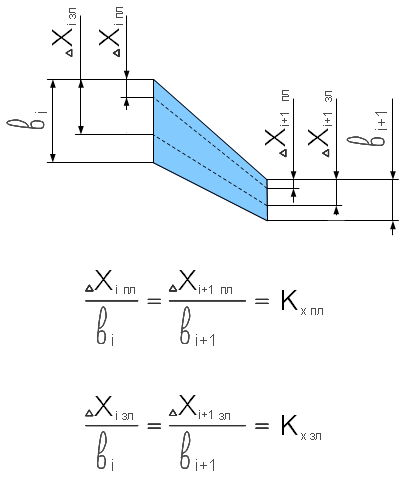
.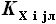 для переднего и заднего лонжеронов кессона как
для переднего и заднего лонжеронов кессона как 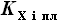 и
и 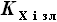 соответственно.
соответственно. 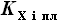 одинаковы. Это означает, что
точки пересечения с передним лонжероном делят длины всех граничных хорд
на части с одним и тем же соотношением. Аналогичное предположение
делаем и относительно заднего лонжерона кессона. Таким образом,
одинаковы. Это означает, что
точки пересечения с передним лонжероном делят длины всех граничных хорд
на части с одним и тем же соотношением. Аналогичное предположение
делаем и относительно заднего лонжерона кессона. Таким образом, 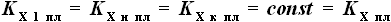 . Аналогично,
. Аналогично, 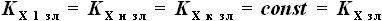 .
.
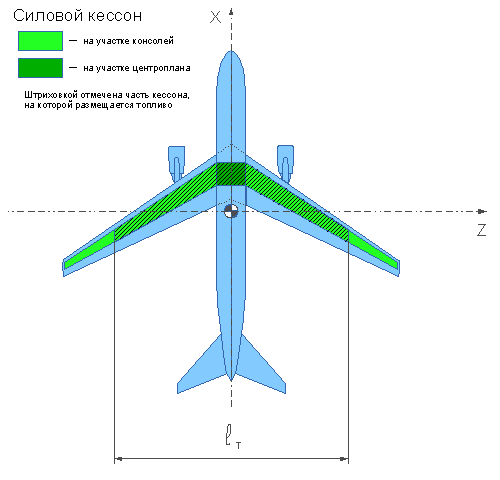
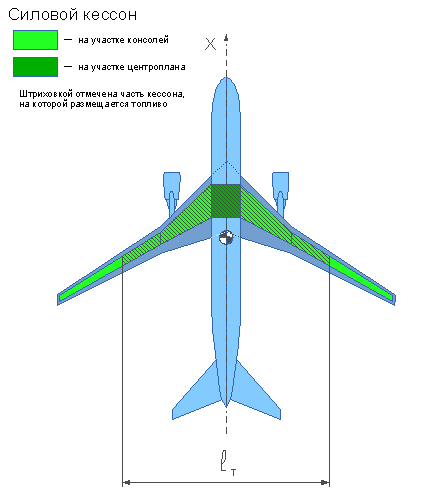
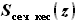 на интервале от z = 0 до z =
на интервале от z = 0 до z = 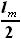 , где
, где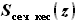 - площадь сечения кессона плоскостью, паралельной XOY и
проходящей через точку z, а
- площадь сечения кессона плоскостью, паралельной XOY и
проходящей через точку z, а 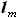 - размах части крыла, имеющей топливные
баки.
- размах части крыла, имеющей топливные
баки.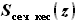 будет
кусочно-заданной). Учитывая это, будем проводить
интегрирование
будет
кусочно-заданной). Учитывая это, будем проводить
интегрирование 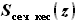 отдельно для каждого фрагмента полукрыла.
отдельно для каждого фрагмента полукрыла.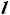 ),
корневой и концевой хорды (
),
корневой и концевой хорды (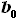 и
и 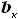 ), а для крыла с наплывом - также
хорды, соответствующей концу наплыва (
), а для крыла с наплывом - также
хорды, соответствующей концу наплыва (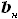 ) и размаха наплыва (
) и размаха наплыва (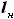 ),
),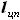 или
или 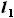 ) и размаха части крыла, имеющей
топливные баки (
) и размаха части крыла, имеющей
топливные баки (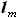 ),
),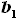 ,
,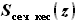 .
.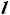 ),
корневая и концевая хорды (
),
корневая и концевая хорды (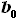 и
и 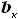 ), а для крыла с наплывом - также хорда, соответствующая концу наплыва (
), а для крыла с наплывом - также хорда, соответствующая концу наплыва (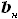 ) и размах части крыла, имеющей наплыв (
) и размах части крыла, имеющей наплыв (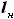 ).
).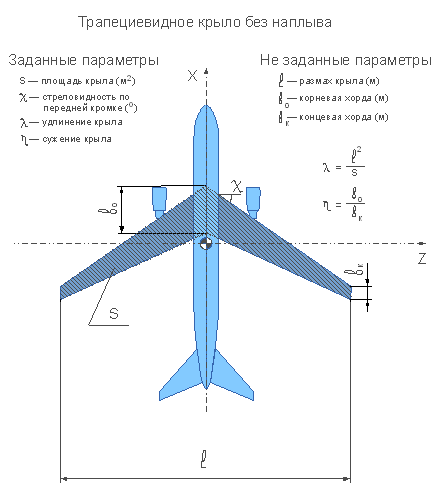
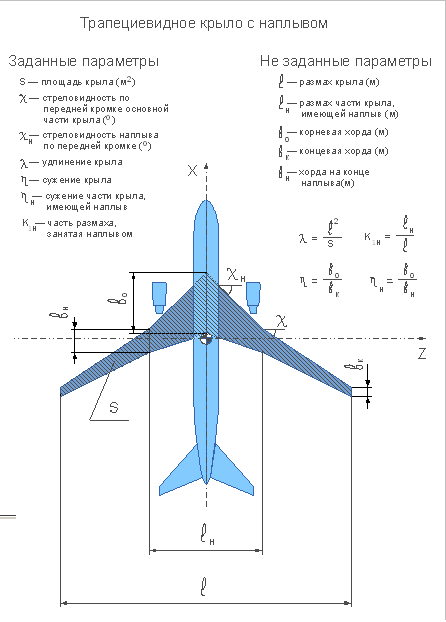
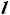 . По определению
. По определению 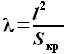 , отсюда следует, что
, отсюда следует, что 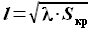 . Параметры
. Параметры 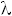 и
и 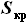 известны, а значит размах крыла
известны, а значит размах крыла 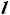 найден. Размах части крыла, имеющей наплыв, тогда можно выразить как
найден. Размах части крыла, имеющей наплыв, тогда можно выразить как 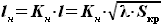 .
.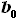 ,
, 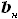 и
и 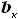 . Учитывая, что
. Учитывая, что 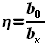 ,
а
,
а 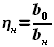 , нам нужно будет найти только
, нам нужно будет найти только 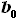 , и тогда
значения
, и тогда
значения 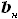 и
и 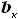 также станут известны:
также станут известны: 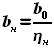 ,
, 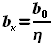 .
.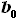 запишем выражение площади крыла
запишем выражение площади крыла 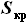 (которая известна
из задания) через размах крыла
(которая известна
из задания) через размах крыла 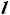 (он тоже известен) и величину
(он тоже известен) и величину 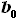 .
.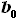 и
и 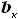 и высотой, равной половине размаха
и высотой, равной половине размаха 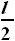 . Известно,
что площадь трапеции равна полусумме оснований, умноженной на высоту.
. Известно,
что площадь трапеции равна полусумме оснований, умноженной на высоту.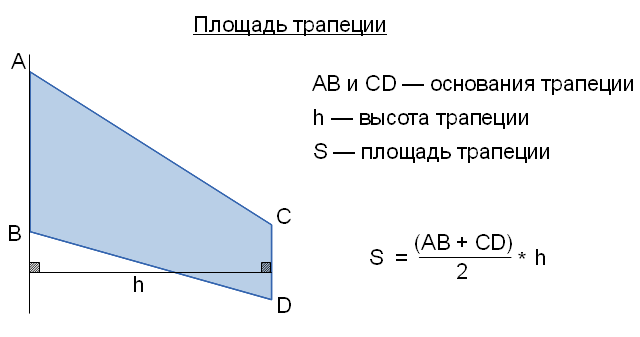
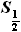 будет равна
будет равна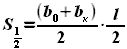
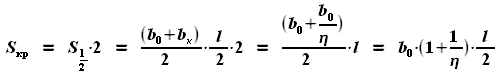
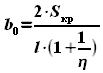
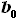 и
и 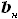 и высотой, равной половине размаха наплывной части
и высотой, равной половине размаха наплывной части 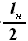 , вторая с основаниями
, вторая с основаниями 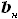 и
и 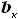 и высотой, равной половине размаха наплывной части
и высотой, равной половине размаха наплывной части 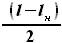 . Соответственно, площадь полукрыла будет равна
. Соответственно, площадь полукрыла будет равна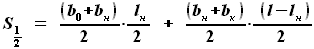
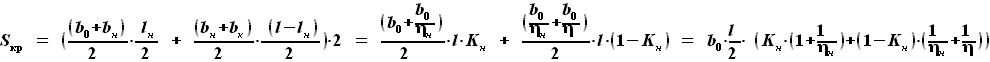
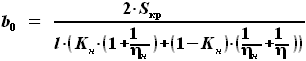
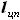 или
или 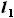 ) и размаха части крыла, имеющей
топливные баки (
) и размаха части крыла, имеющей
топливные баки (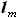 ).
).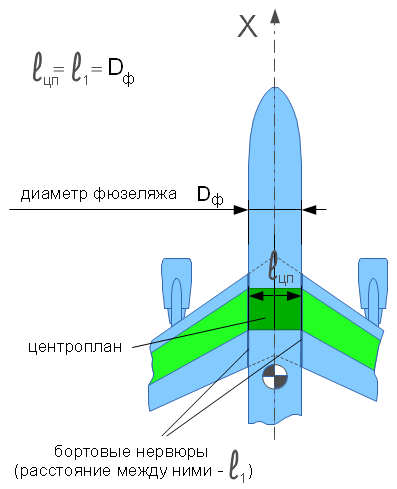
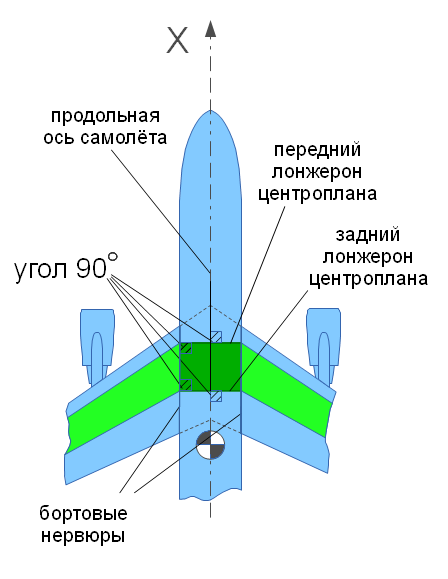
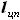 - размах центроплана совпадает с
- размах центроплана совпадает с 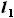 - расстоянием между бортовыми
нервюрами (по крайней мере, в нашей расчётой схеме). Условно можно
считать, что они равны диаметру фюзеляжа
- расстоянием между бортовыми
нервюрами (по крайней мере, в нашей расчётой схеме). Условно можно
считать, что они равны диаметру фюзеляжа 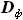 . Ни одно из этих значений
нам не задано и они не выводятся из известных параметров, а значит,
необходимо выбрать их самостоятельно. Так как мы условились вводить
новые значения только в форме безразмерных коэффициентов, то представим
. Ни одно из этих значений
нам не задано и они не выводятся из известных параметров, а значит,
необходимо выбрать их самостоятельно. Так как мы условились вводить
новые значения только в форме безразмерных коэффициентов, то представим 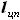 как часть размаха крыла
как часть размаха крыла 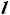 .
.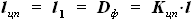 ,
,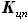 - задаваемое нами отношение ширины центроплана к полному размаху крыла.
- задаваемое нами отношение ширины центроплана к полному размаху крыла.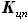 мы будем выбирать ориентируясь на реально существующие самолёты.
мы будем выбирать ориентируясь на реально существующие самолёты.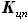 , характерное именно для самолётов, близких по
конструкции и назначению.
, характерное именно для самолётов, близких по
конструкции и назначению. 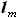 - размах той части крыла, на которой есть топливные баки. Эта
величина нам также неизвестна и её мы также зададим через коэффициент
отношения к полному размаху крыла
- размах той части крыла, на которой есть топливные баки. Эта
величина нам также неизвестна и её мы также зададим через коэффициент
отношения к полному размаху крыла 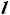 .
.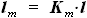 ,
,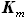 - коэффициент, показывающий, какую часть полного размаха крыла занимают топливные баки.
- коэффициент, показывающий, какую часть полного размаха крыла занимают топливные баки.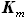 выбираем при расчёте ориентируясь на ЛА сходной конструкции и имеющие
близкую геометрию крыла. При этом, учитывая, что для крыла с наплывом
топливные баки занимают часть размаха большую чем размах участков,
имеющих наплыв,
выбираем при расчёте ориентируясь на ЛА сходной конструкции и имеющие
близкую геометрию крыла. При этом, учитывая, что для крыла с наплывом
топливные баки занимают часть размаха большую чем размах участков,
имеющих наплыв, 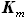 должен быть больше чем
должен быть больше чем 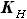 .
.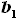 .
.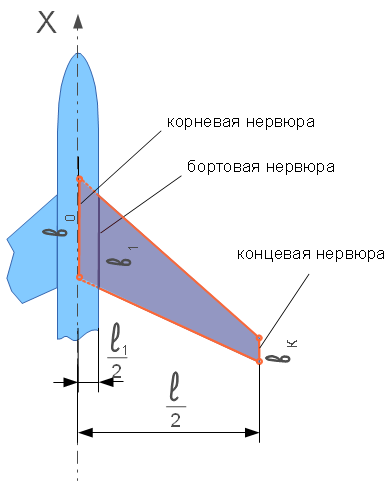
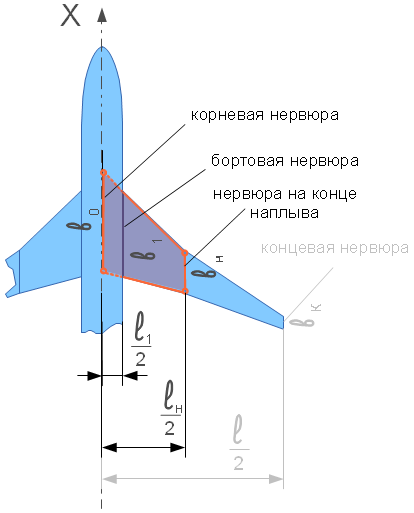
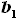 это хорда крыла, располагающаяся на расстоянии
это хорда крыла, располагающаяся на расстоянии 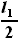 от оси симметрии. Геометрия крыльев, оговоренная в задании,
такова, что хорда
от оси симметрии. Геометрия крыльев, оговоренная в задании,
такова, что хорда 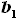 находится на участке крыла, имеющего форму
трапеции с основаниями
находится на участке крыла, имеющего форму
трапеции с основаниями 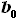 и
и 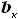 в варианте без наплыва или
в варианте без наплыва или 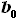 и
и 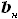 в
варианте с наплывом. Высота трапеции будет равна
в
варианте с наплывом. Высота трапеции будет равна 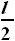 (вариант без
наплыва) или
(вариант без
наплыва) или 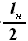 (вариант с наплывом).
(вариант с наплывом).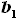 , но и
вообще зависимость хорды от размаха на произвольном трапециевидном
фрагменте крыла.
, но и
вообще зависимость хорды от размаха на произвольном трапециевидном
фрагменте крыла.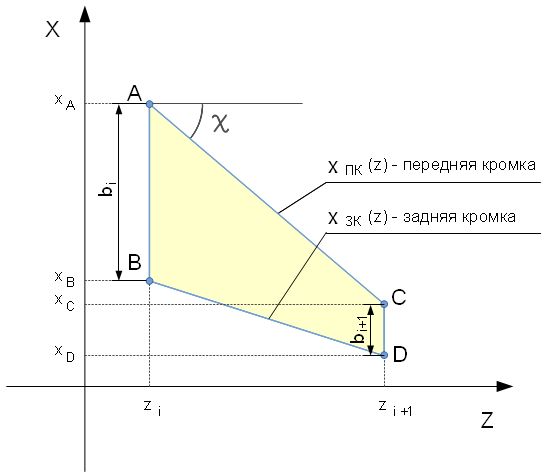
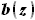 будет равна расстоянию между передней и задней кромками, то есть, разности функций
будет равна расстоянию между передней и задней кромками, то есть, разности функций 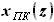 и
и 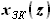 ,
,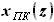 - функция, описывающая положение передней кромки крыла на участке от
- функция, описывающая положение передней кромки крыла на участке от 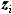 до
до 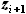
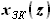 - функция, описывающая положение задней кромки крыла на участке от
- функция, описывающая положение задней кромки крыла на участке от 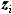 до
до 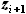
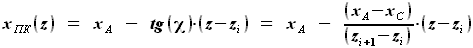
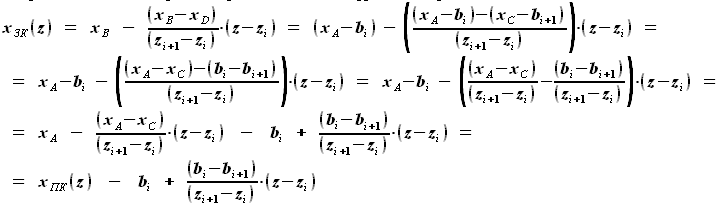
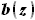 на участке от
на участке от 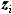 до
до 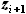 будет равна
будет равна 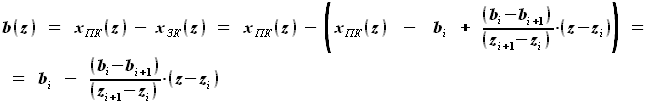
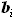 и
и 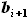 и расстояния между ними
и расстояния между ними 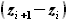 .
Координаты
.
Координаты 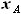 и
и 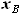 (и выражаемые через них
(и выражаемые через них 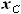 и
и 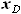 ) не входят в
) не входят в 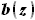 , то есть, имеют значение только расстояния между точками A, B, C и
D, а не их абсолютные координаты на плоскости XZ (что, в общем-то,
очевидно). Отметим также, что в выражении
, то есть, имеют значение только расстояния между точками A, B, C и
D, а не их абсолютные координаты на плоскости XZ (что, в общем-то,
очевидно). Отметим также, что в выражении 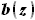 присутствуют разность
координат по оси X между A и B (это
присутствуют разность
координат по оси X между A и B (это 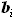 ) и между C и D (это
) и между C и D (это 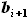 ), а
расстояние по X между точками A и C, как и равное ему расстояние между
B и D, - отсутствуют. А так как именно разность
), а
расстояние по X между точками A и C, как и равное ему расстояние между
B и D, - отсутствуют. А так как именно разность 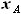 и
и 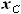 определяет
стреловидность фрагмента крыла при его фиксированном размахе
определяет
стреловидность фрагмента крыла при его фиксированном размахе 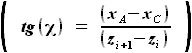 , то получается, что длина местной хорды
, то получается, что длина местной хорды 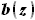 не зависит от угла стреловидности.
не зависит от угла стреловидности.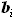 и
и 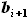 значения
значения 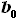 и
и 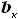 ,
а вместо
,
а вместо 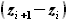 и
и 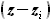 значения
значения 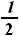 и
и 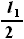 мы получим
величину
мы получим
величину 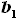 для крыла без наплыва.
для крыла без наплыва.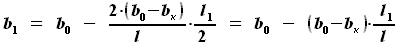
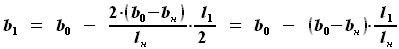
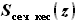 . Для этого сначала рассмотрим зависимость
. Для этого сначала рассмотрим зависимость 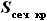 - площади сечения всего крыла (не только кессона) от z.
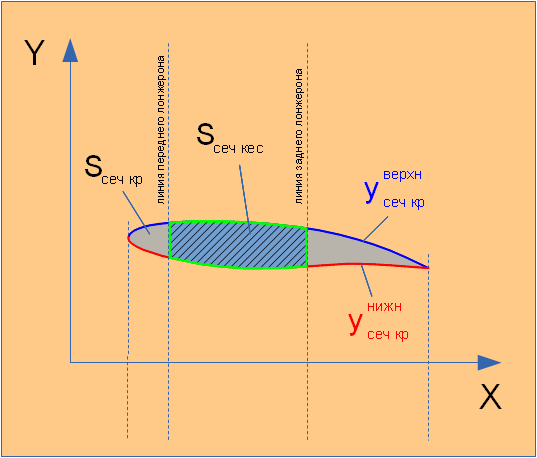
- площади сечения всего крыла (не только кессона) от z.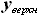 и
и 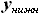 ,
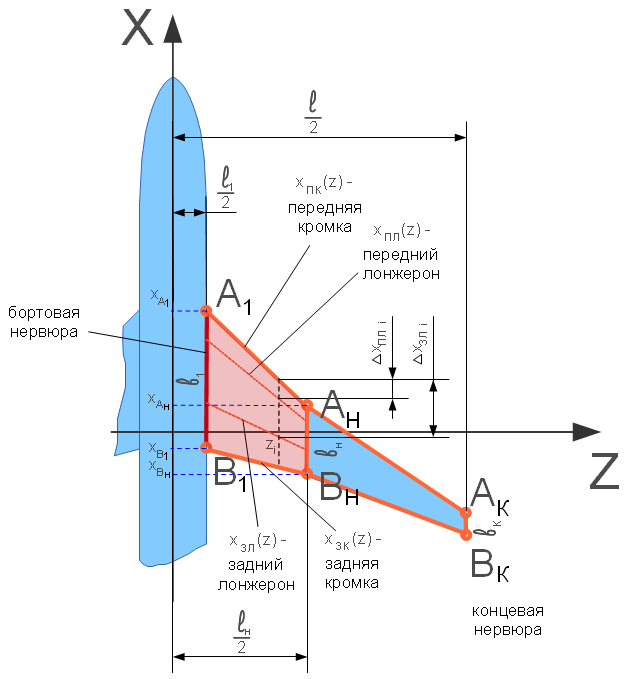
образующие верхнюю и нижнюю границы.
,
образующие верхнюю и нижнюю границы. 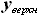 и
и 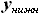 соединяются в
самой передней точке профиля A (на его носке) и в самой задней точке B
(см. рисунок).
соединяются в
самой передней точке профиля A (на его носке) и в самой задней точке B
(см. рисунок).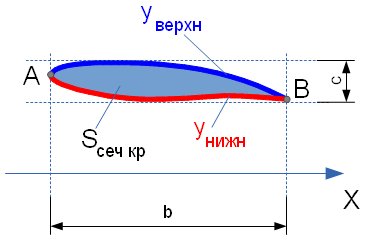
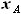 до
до 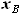 .
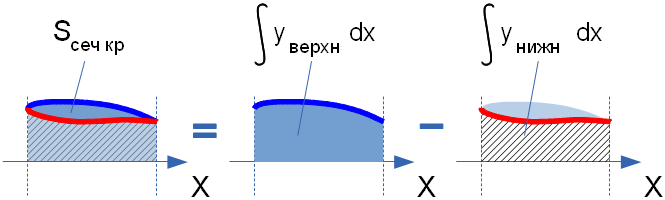
.
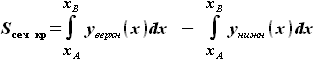
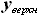 и
и 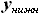 обычно в виде таблицы для профиля с длиной
хорды b = 1 и помещённого носком в начало координат. В этом случае
выражение для площади такого табличного сечения
обычно в виде таблицы для профиля с длиной
хорды b = 1 и помещённого носком в начало координат. В этом случае
выражение для площади такого табличного сечения 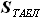 имеет вид
имеет вид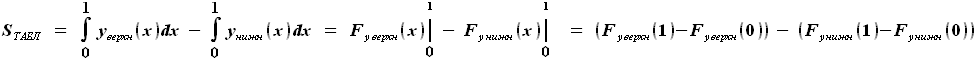
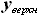 и
и 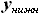 , представим
, представим 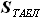 как часть площади описанного прямоугольника:
как часть площади описанного прямоугольника: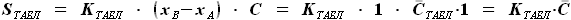 ,
, 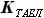 - коэффициент, показывающий, какую часть занимает площадь профиля крыла от площади описанного прямоугольника (со сторонами b=1 и
- коэффициент, показывающий, какую часть занимает площадь профиля крыла от площади описанного прямоугольника (со сторонами b=1 и 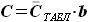 ), величину этого коэффициента мы задаём эмпирически,
), величину этого коэффициента мы задаём эмпирически,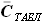 - относительная толщина профиля, для которого заданы табличные значения
- относительная толщина профиля, для которого заданы табличные значения 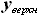 и
и 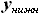 .
.
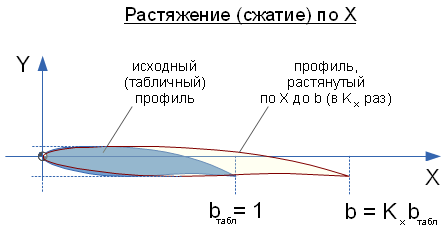
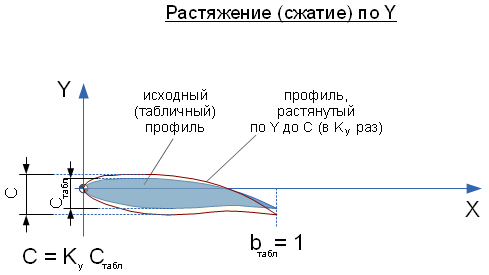
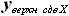 и
и 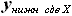 , которые могут быть выражены как:
, которые могут быть выражены как: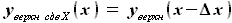 и
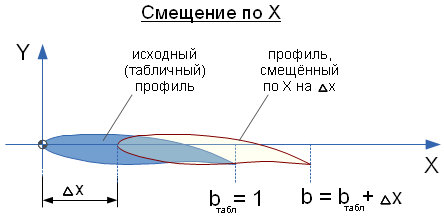
и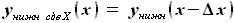 ,
,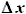 - смещение носка профиля по X от начала координат
- смещение носка профиля по X от начала координат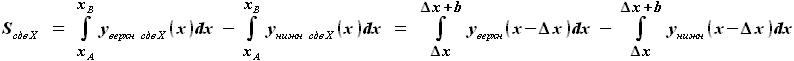
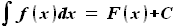 , то
, то 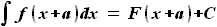
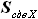 =
=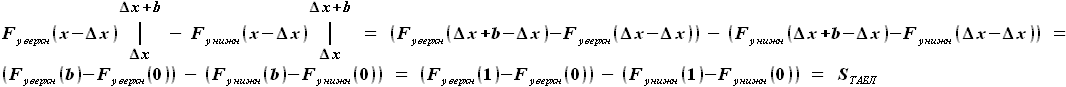
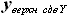 и
и 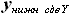 , которые могут быть выражены как:
, которые могут быть выражены как: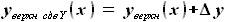 и
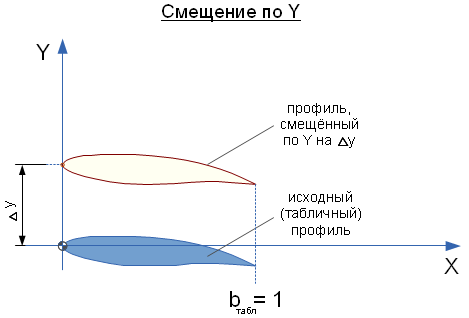
и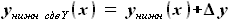 ,
,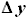 - смещение носка профиля по Y от начала координат
- смещение носка профиля по Y от начала координат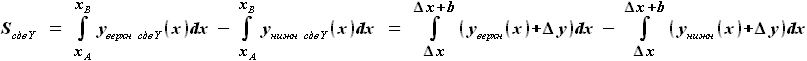
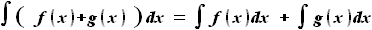 ,
,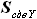 =
=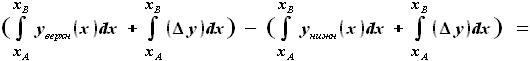
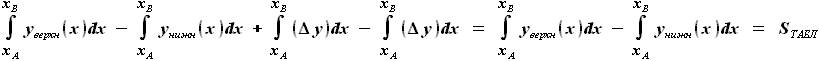
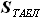 ) не изменяется при любых перемещениях его в плоскости XY.
Соответственно, как бы ни был профиль сдвинут по вертикали или
горизонтали, его площадь можно рассчитывать так же, как если бы он
находился в исходном положении - носком в начале координат.
) не изменяется при любых перемещениях его в плоскости XY.
Соответственно, как бы ни был профиль сдвинут по вертикали или
горизонтали, его площадь можно рассчитывать так же, как если бы он
находился в исходном положении - носком в начале координат.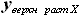 и
и 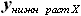 , которые могут быть выражены как:
, которые могут быть выражены как: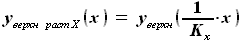 и
и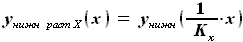 ,
,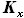 - коэффициент растяжения профиля по оси X. Этот коэффициент равен
- коэффициент растяжения профиля по оси X. Этот коэффициент равен 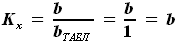
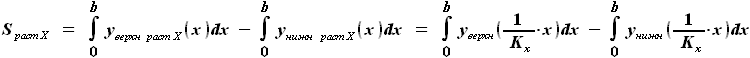
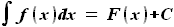 , то
, то 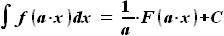
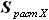 =
=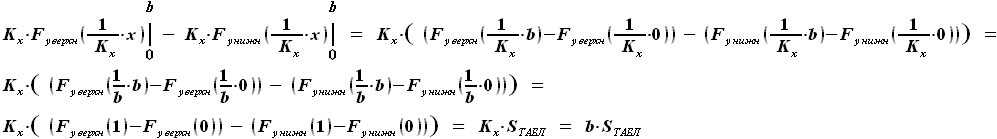
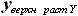 и
и 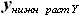 , которые могут быть выражены как:
, которые могут быть выражены как: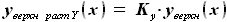 и
и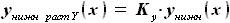 ,
,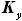 - коэффициент растяжения профиля по оси Y. Этот коэффициент равен
- коэффициент растяжения профиля по оси Y. Этот коэффициент равен 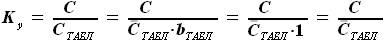
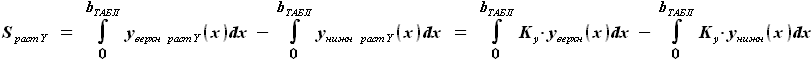
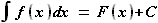 , то
, то 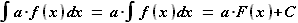
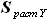 =
=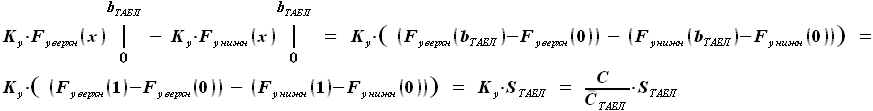
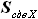 =
= 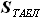 ,
,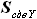 =
= 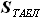 ,
,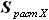 =
= 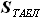 *
* 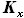 ,
,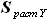 =
= 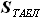 *
* 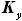 ,
,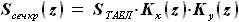
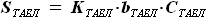 , а
, а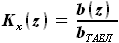 и
и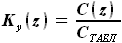 ,
,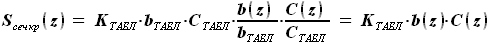
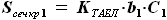
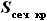 найдено, приступим к определению зависимости от z площади сечения кессоной части крыла
найдено, приступим к определению зависимости от z площади сечения кессоной части крыла 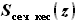 .
.
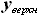 и
и 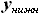 , но пределами интегрирования будут не координаты носка и конца профиля, а координаты линий переднего и заднего лонжеронов.
, но пределами интегрирования будут не координаты носка и конца профиля, а координаты линий переднего и заднего лонжеронов.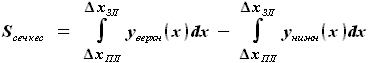 , где
, где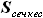 - площадь сечения кессонной части крыла по координате z,
- площадь сечения кессонной части крыла по координате z,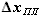 - расстояние от носка до переднего лонжерона в сечении по координате z,
- расстояние от носка до переднего лонжерона в сечении по координате z,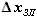 - расстояние от носка до заднего лонжерона в сечении по координате z,
- расстояние от носка до заднего лонжерона в сечении по координате z,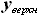 и
и 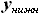 - верхняя и нижняя линии сечения крыла по координате z
- верхняя и нижняя линии сечения крыла по координате z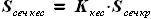 , где
, где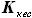 - коэффициент, указывающий, какую долю от площади данного сечения крыла
- коэффициент, указывающий, какую долю от площади данного сечения крыла 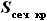 составляет площадь кессонной части.
составляет площадь кессонной части.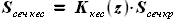
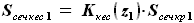 , где
, где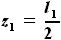 - координата z сечения крыла по бортовой нервюре
- координата z сечения крыла по бортовой нервюре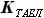 ,
здесь можно задать значение для
,
здесь можно задать значение для 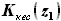 , ориентируясь на
примеры реально существующих ЛА. Обозначим это число как
, ориентируясь на
примеры реально существующих ЛА. Обозначим это число как 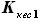 .
.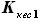 - доля, которую составляет кессонная часть от общей площади сечения крыла по бортовой нервюре.
- доля, которую составляет кессонная часть от общей площади сечения крыла по бортовой нервюре.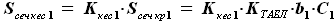
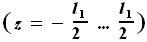 площадь сечения кессона равна:
площадь сечения кессона равна: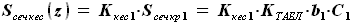
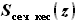 на трапециевидных фрагментах крыла.
на трапециевидных фрагментах крыла.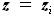 . Обозначим его как i-е сечение. После
переноса его носком профиля в начало координат (ранее было доказано,
что площадь при этом не меняется), площадь кессонной части определяется выражением:
. Обозначим его как i-е сечение. После
переноса его носком профиля в начало координат (ранее было доказано,
что площадь при этом не меняется), площадь кессонной части определяется выражением: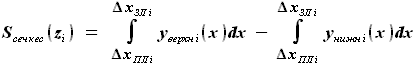 , где
, где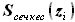 или
или 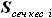 - площадь сечения кессонной части крыла по координате
- площадь сечения кессонной части крыла по координате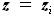 ,
,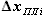 - расстояние от носка до переднего лонжерона в сечении по координате
- расстояние от носка до переднего лонжерона в сечении по координате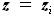 ,
,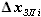 - расстояние от носка до заднего лонжерона в сечении по координате
- расстояние от носка до заднего лонжерона в сечении по координате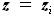 ,
,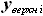 и
и 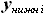 - верхняя и нижняя линии сечения крыла по координате
- верхняя и нижняя линии сечения крыла по координате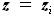
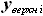 и
и 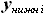 можно выразить через линии сечения крыла по бортовой нервюре:
можно выразить через линии сечения крыла по бортовой нервюре: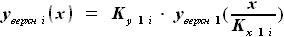 и
и 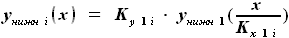 , где
, где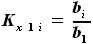 - коэффициент масштабирования по хорде (оси X) i-го сечения по сравнению с сечением по бортовой непвюре
- коэффициент масштабирования по хорде (оси X) i-го сечения по сравнению с сечением по бортовой непвюре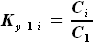 - коэффициент масштабирования по толщине (оси Y) i-го сечения по сравнению с сечением по бортовой непвюре
- коэффициент масштабирования по толщине (оси Y) i-го сечения по сравнению с сечением по бортовой непвюре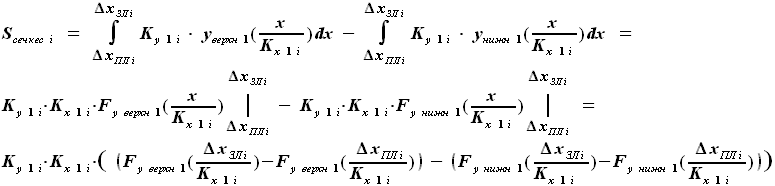
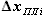 и
и 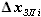 - расстояния от носка до, соответственно, переднего и заднего лонжеронов.
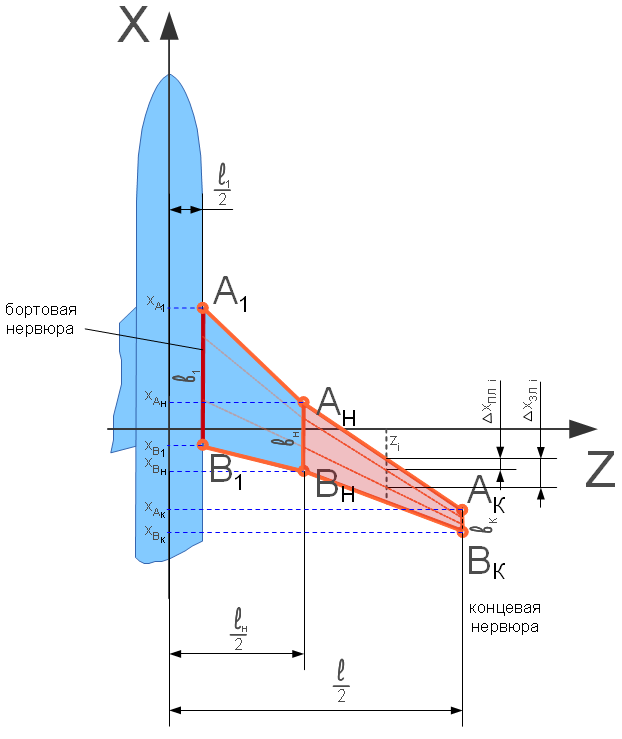
- расстояния от носка до, соответственно, переднего и заднего лонжеронов.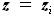 функций, описывающих линию передней кромки
функций, описывающих линию передней кромки 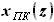 и линию лонжерона. Запишем эти функции и выразим их разность. Кроме того, запишем функцию линии задней кромки
и линию лонжерона. Запишем эти функции и выразим их разность. Кроме того, запишем функцию линии задней кромки 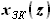 , с её помощью найдём выражение для хорды крыла
, с её помощью найдём выражение для хорды крыла 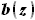 (длина хорды равна разнице координат передней и задней кромок) и постараемся выразить
(длина хорды равна разнице координат передней и задней кромок) и постараемся выразить 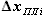 и
и 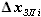 через длину хорды.
через длину хорды.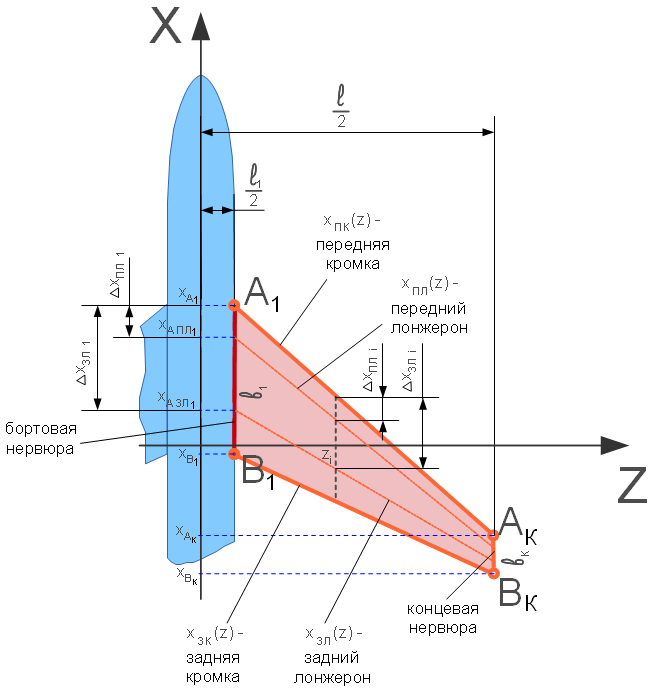
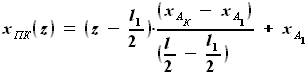
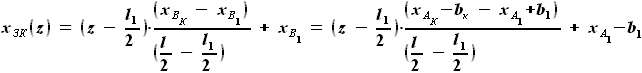
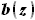 выражается как разность
выражается как разность 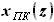 и
и 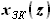 :
: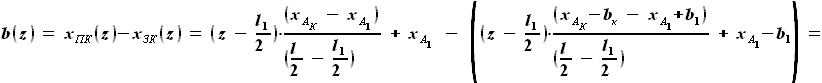
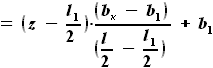
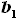 и
и 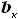 , расстояние от передней кромки до переднего лонжерона равно
, расстояние от передней кромки до переднего лонжерона равно 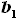
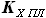 и
и 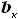
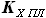 (см. описание расчётной схемы):
(см. описание расчётной схемы):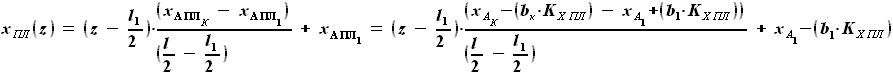
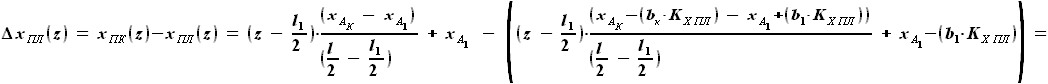
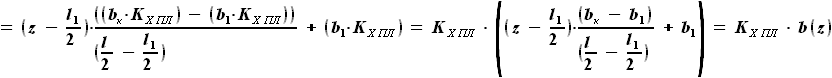
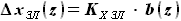
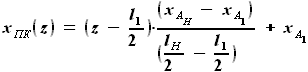
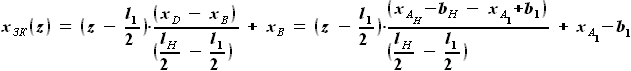
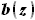 выражается как разность
выражается как разность 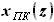 и
и 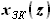 :
: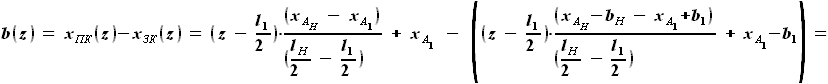
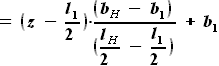
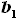 и
и 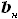 , расстояние от передней кромки до переднего лонжерона равно
, расстояние от передней кромки до переднего лонжерона равно 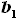
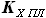 и
и 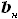
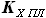 (см. описание расчётной схемы):
(см. описание расчётной схемы):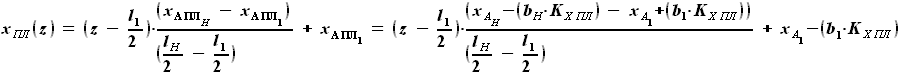
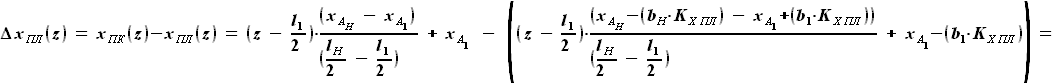
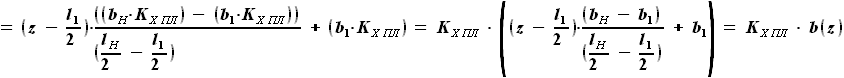
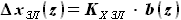
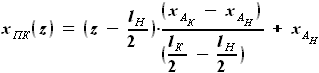
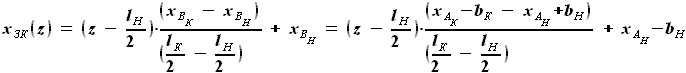
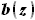 выражается как разность
выражается как разность 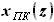 и
и 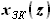 :
: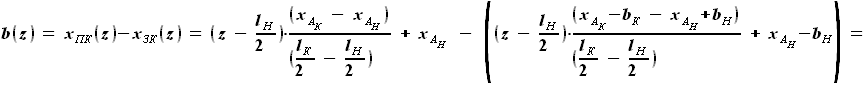
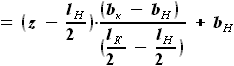
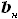 и
и 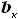 , расстояние от передней кромки до переднего лонжерона равно
, расстояние от передней кромки до переднего лонжерона равно 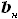
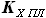 и
и 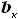
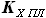 (см. описание расчётной схемы):
(см. описание расчётной схемы):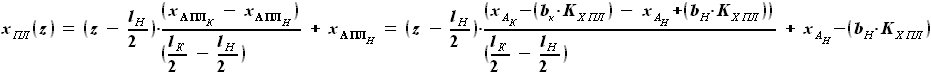
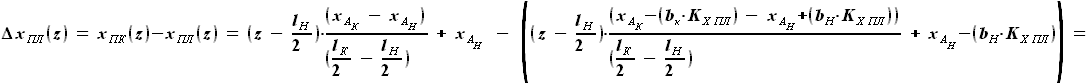
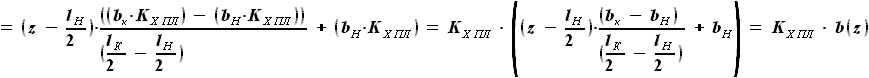
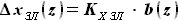
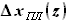 и
и 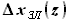 выражаются через хорду крыла:
выражаются через хорду крыла: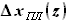 =
= 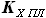
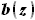
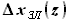 =
= 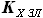
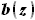
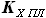 и
и 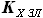 .
.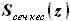 , она же
, она же 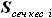
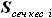 :
: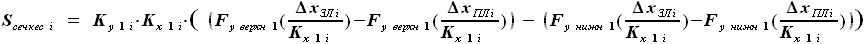 , где
, где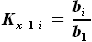
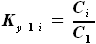
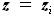 трапециевидного фрагмента нашего крыла справедливо
трапециевидного фрагмента нашего крыла справедливо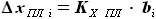
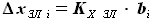
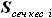 будет иметь вид:
будет иметь вид: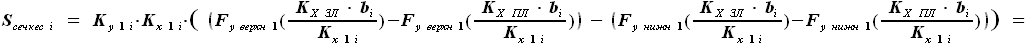
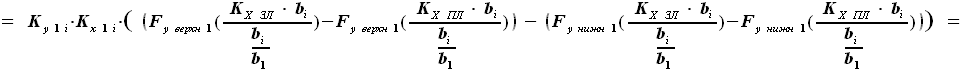
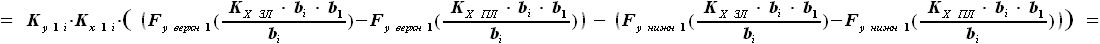
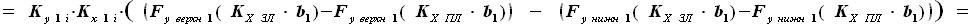
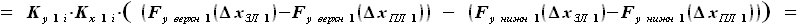
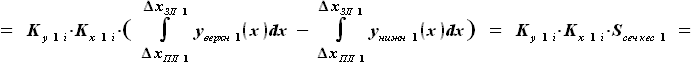
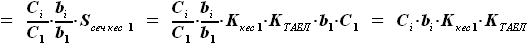
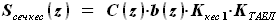
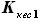 и
и 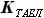 - выбираемые нами константы, их произведение можно заменить на один коэффициент, обозначим его
- выбираемые нами константы, их произведение можно заменить на один коэффициент, обозначим его 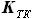 . Величина
. Величина 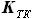 - это часть, которую составляет площадь кессонной части крыла от площади прямоугольника со сторонами
- это часть, которую составляет площадь кессонной части крыла от площади прямоугольника со сторонами 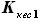 и
и 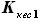 , в который вписано сечение крыла. Как показано выше, величина
, в который вписано сечение крыла. Как показано выше, величина 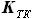 одна и та же для всех сечений, то есть, она не зависит от координаты z, по которой проходит сечение (в пределах
одна и та же для всех сечений, то есть, она не зависит от координаты z, по которой проходит сечение (в пределах 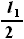 ..
.. 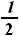 ).
).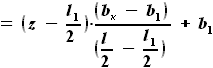 ,
,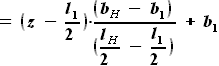
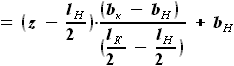
 - толщина крыла, выражается через хорду
- толщина крыла, выражается через хорду 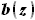 и относительную толщину
и относительную толщину 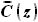 :
: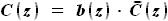
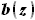 уже было детально описано выше, а
уже было детально описано выше, а 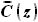 определяется исходя из задания: относительная толщина меняется линейно
от
определяется исходя из задания: относительная толщина меняется линейно
от 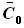 у корня до
у корня до 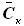 на конце, то есть:
на конце, то есть: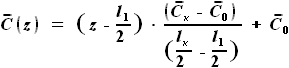
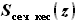 , на этом можно считать завершённым этап предварительных расчётов и
приступать непосредственно к расчёту объёмов топливных баков.
, на этом можно считать завершённым этап предварительных расчётов и
приступать непосредственно к расчёту объёмов топливных баков.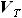 . Он равен объёму части кессона, отведённой под баки, умноженной на коэффициент заполнения
. Он равен объёму части кессона, отведённой под баки, умноженной на коэффициент заполнения 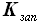 .
.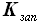 берём равным 0.85 для гражданских самолётов и 0.75
для военных. У военных значение меньше так как оно учитывает, что в баках
находится пенополиуретановый заполнитель, препятствующий взрыву при
прострелах.
берём равным 0.85 для гражданских самолётов и 0.75
для военных. У военных значение меньше так как оно учитывает, что в баках
находится пенополиуретановый заполнитель, препятствующий взрыву при
прострелах.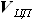 и объёмов топливной части кессона консолей левого и правого полукрыльев
и объёмов топливной части кессона консолей левого и правого полукрыльев 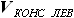 и
и 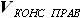 . Так как самолёт у нас симметричен относительно плоскости XOY,
то объёмы топливной части кессона консолей обеих полукрыльев будут
одинаковы. Обозначим объём баковой части кессона консоли одного
полукрыла как
. Так как самолёт у нас симметричен относительно плоскости XOY,
то объёмы топливной части кессона консолей обеих полукрыльев будут
одинаковы. Обозначим объём баковой части кессона консоли одного
полукрыла как 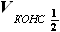 . Тогда объём топлива
. Тогда объём топлива 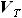 будет равен сумме объёма центроплана
будет равен сумме объёма центроплана 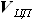 и двух объёмов
и двух объёмов 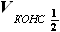 , умноженной на
, умноженной на 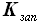 . Учитывая, что центроплан также симметричен относительно XOY, можно представить это выражение как
. Учитывая, что центроплан также симметричен относительно XOY, можно представить это выражение как 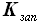 , умноженное на удвоенную сумму половины объёма центроплана
, умноженное на удвоенную сумму половины объёма центроплана 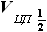 и объёма
и объёма 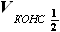 .
.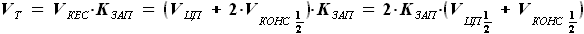
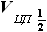 - объёма половины центроплана и
- объёма половины центроплана и 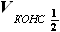 - объёма топливной части кессона консоли одного полукрыла.
- объёма топливной части кессона консоли одного полукрыла.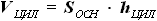 ,
, 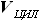 - объём цилиндра
- объём цилиндра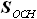 - площадь основания цилиндра
- площадь основания цилиндра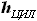 - высота цилиндра
- высота цилиндра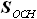 будет являться площадь сечения центроплана, она же площадь сечения кессона крыла по бортовой нервюре
будет являться площадь сечения центроплана, она же площадь сечения кессона крыла по бортовой нервюре 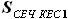 , а высотою
, а высотою 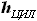 - половина размаха центроплана
- половина размаха центроплана 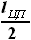 . Тогда объём половины центроплана будет равен:
. Тогда объём половины центроплана будет равен: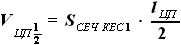
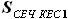 и
и 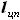 ранее уже были найдены выражения:
ранее уже были найдены выражения: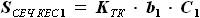
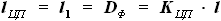
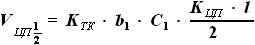
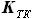 и
и 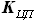 выбираются нами эмпирически, а остальные -
выбираются нами эмпирически, а остальные - 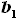 ,
, 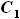 и l выразим через другие величины:
и l выразим через другие величины: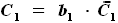
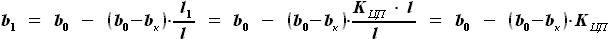
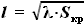
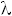 ,
, 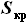 и
и 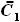 заданы в условии, а
заданы в условии, а 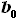 и
и 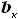 выражаются через них и через
выражаются через них и через 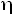 , которая тоже задана в условии:
, которая тоже задана в условии: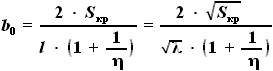
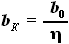
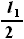 , а конечной границей - координата окончания топливного бака
, а конечной границей - координата окончания топливного бака 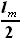 .
.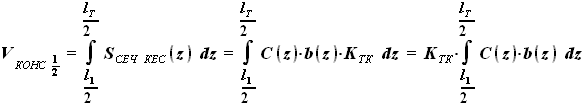 ,
, 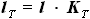 ,
,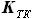 и
и 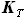 - выбираемые нами параметры. Для функций b(z) и C(z) выражения были найдены ранее:
- выбираемые нами параметры. Для функций b(z) и C(z) выражения были найдены ранее: 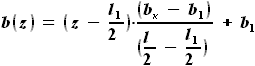
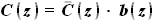 ,
,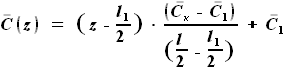
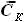 и
и 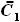 - параметры, заданные в условии.
- параметры, заданные в условии.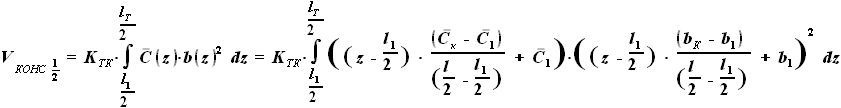
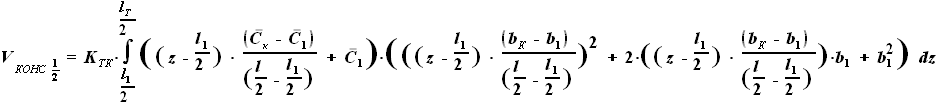
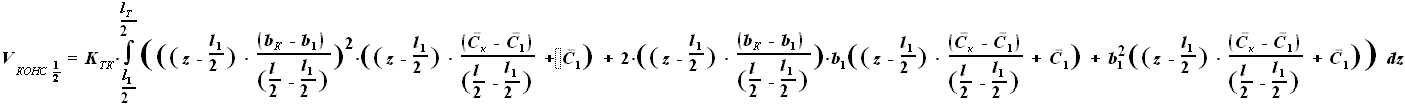
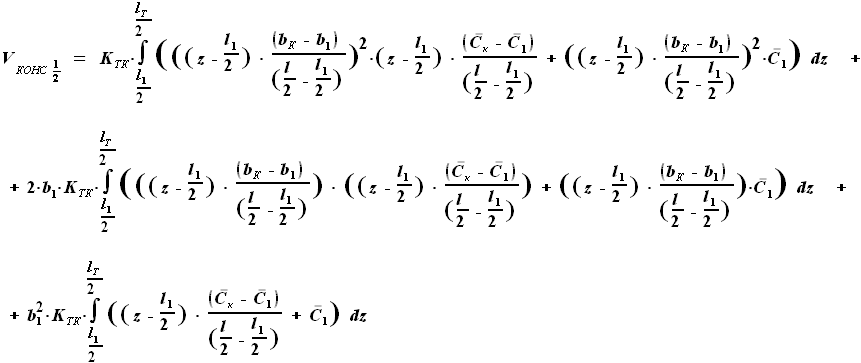
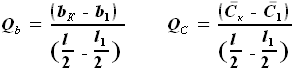
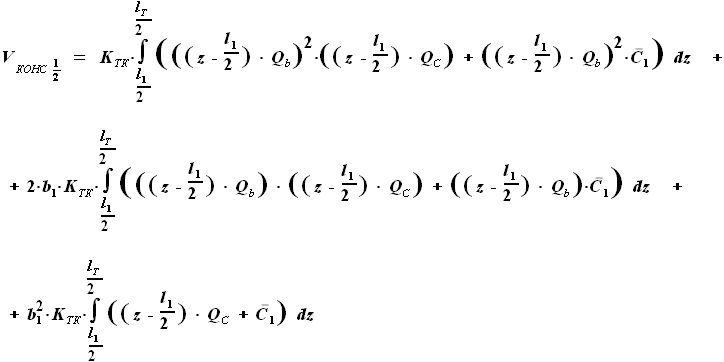
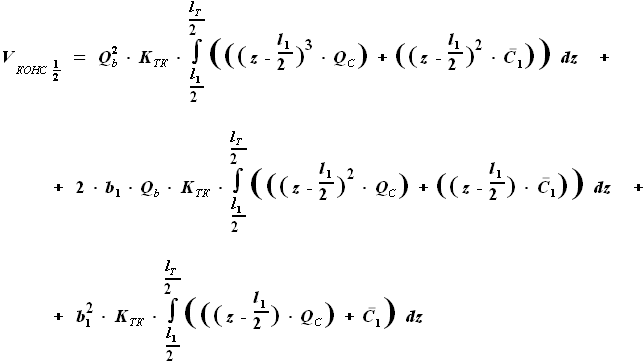
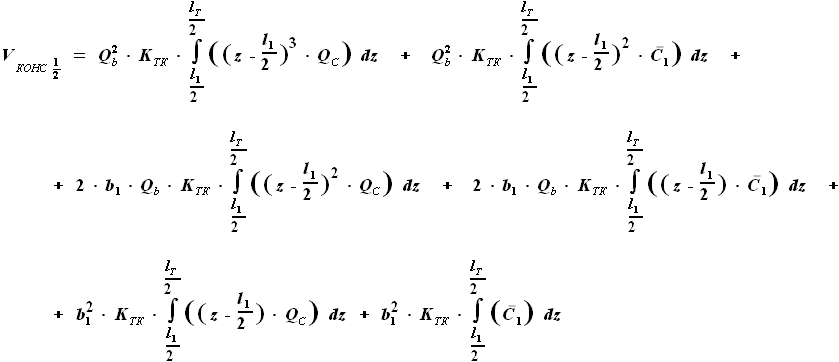
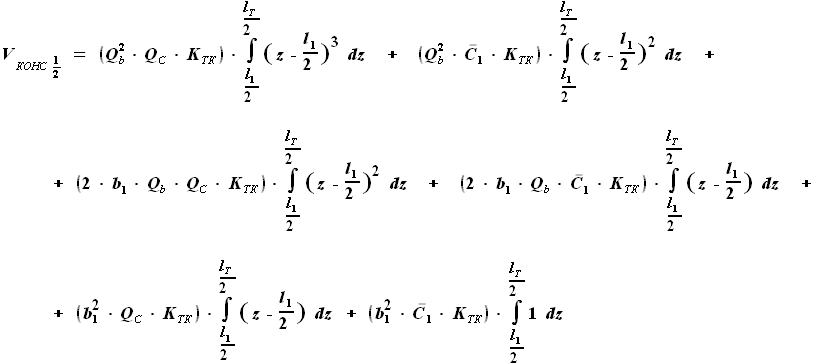
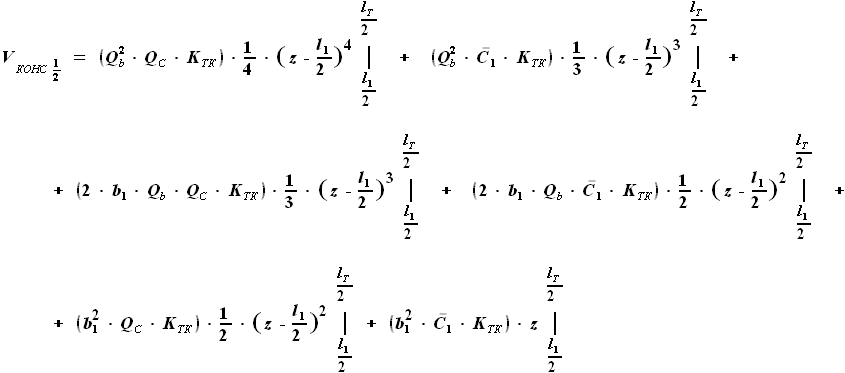
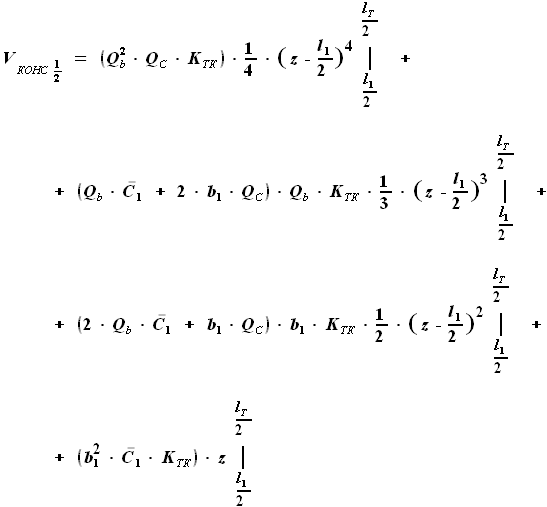
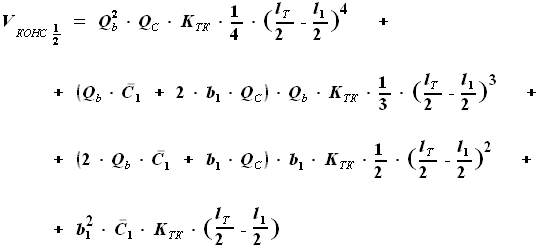
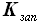 , умноженное на удвоенную сумму половины объёма центроплана
, умноженное на удвоенную сумму половины объёма центроплана 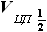 и объёма
и объёма 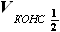 .
Но для проведения удобства проведения расчёта, консоль крыла мы
разделим на часть имеющую наплыв и часть вне наплыва. Соответственно,
объём топливной части кессона консоли
.
Но для проведения удобства проведения расчёта, консоль крыла мы
разделим на часть имеющую наплыв и часть вне наплыва. Соответственно,
объём топливной части кессона консоли 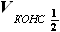 будет состоять из объёма на участке наплыва
будет состоять из объёма на участке наплыва 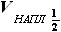 и объёма на участке, не имеющем наплыва
и объёма на участке, не имеющем наплыва 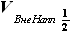 .
.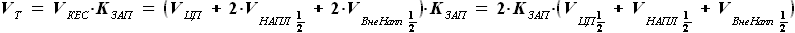
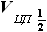 - объёма половины центроплана,
- объёма половины центроплана,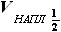 - объёма топливной части кессона полукрыла на участке наплыва и
- объёма топливной части кессона полукрыла на участке наплыва и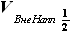 - топливной части кессона полукрыла вне участка наплыва.
- топливной части кессона полукрыла вне участка наплыва.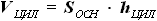 ,
, 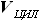 - объём цилиндра
- объём цилиндра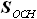 - площадь основания цилиндра
- площадь основания цилиндра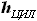 - высота цилиндра
- высота цилиндра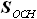 будет являться площадь сечения центроплана, она же площадь сечения кессона крыла по бортовой нервюре
будет являться площадь сечения центроплана, она же площадь сечения кессона крыла по бортовой нервюре 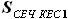 , а высотою
, а высотою 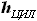 - половина размаха центроплана
- половина размаха центроплана 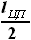 . Тогда объём половины центроплана будет равен:
. Тогда объём половины центроплана будет равен: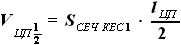
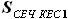 и
и 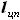 ранее уже были найдены выражения:
ранее уже были найдены выражения: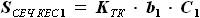
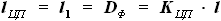
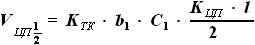
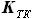 и
и 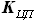 выбираются нами эмпирически, а остальные -
выбираются нами эмпирически, а остальные - 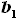 ,
, 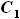 и l выразим через другие величины:
и l выразим через другие величины: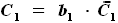
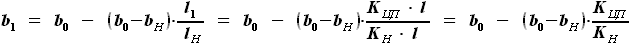
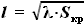
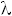 ,
, 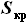 ,
, 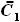 и
и 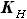 заданы в условии, а
заданы в условии, а 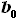 и
и 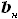 выражаются через них и через
выражаются через них и через 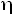 и
и 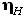 , которые тоже заданы в условии:
, которые тоже заданы в условии: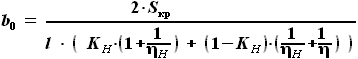
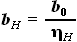
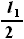 .
Так как топливные баки располагаются на протяжении всего размаха
участка наплыва, то конечной границей будет являться координата
окончания участка
.
Так как топливные баки располагаются на протяжении всего размаха
участка наплыва, то конечной границей будет являться координата
окончания участка 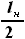 .
.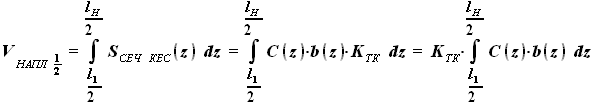 ,
, 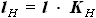 ,
,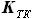 - выбираемый нами параметр, а
- выбираемый нами параметр, а 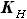 - задан в условии. Для функций b(z) и C(z) выражения были найдены ранее:
- задан в условии. Для функций b(z) и C(z) выражения были найдены ранее: 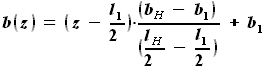
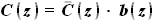 ,
,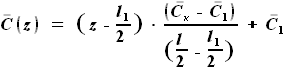
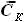 и
и 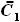 - параметры, заданные в условии.
- параметры, заданные в условии.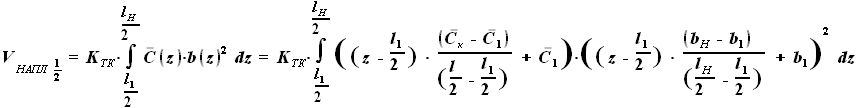
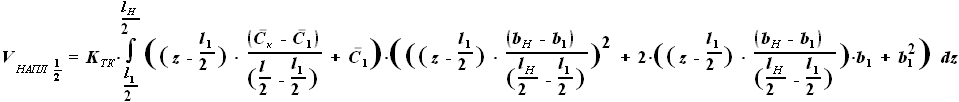
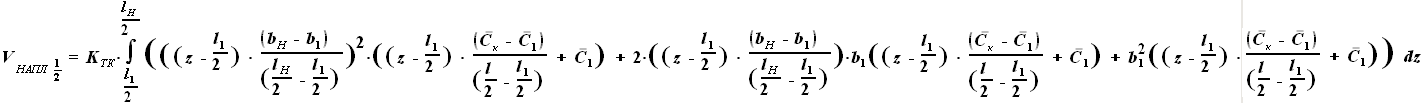
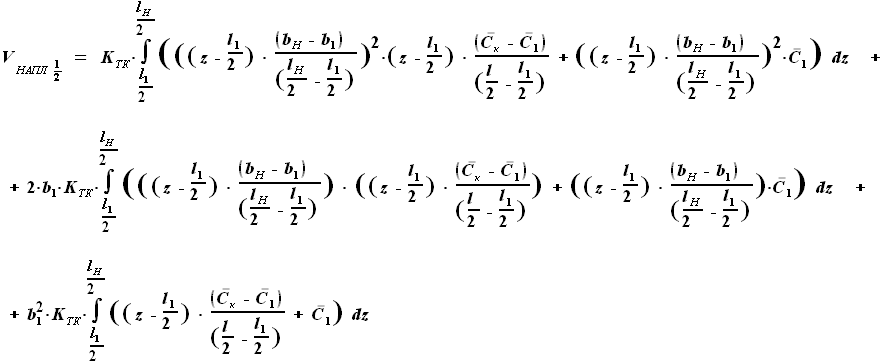
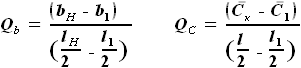
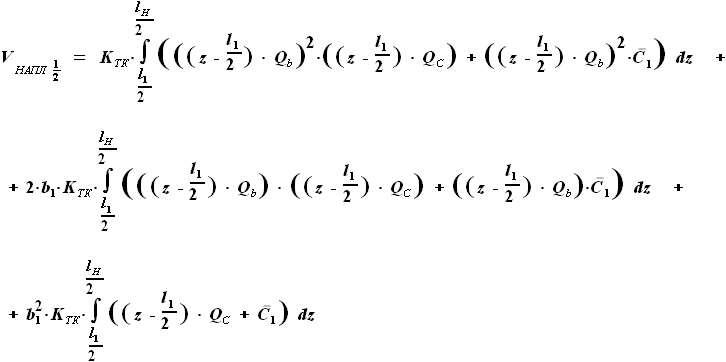
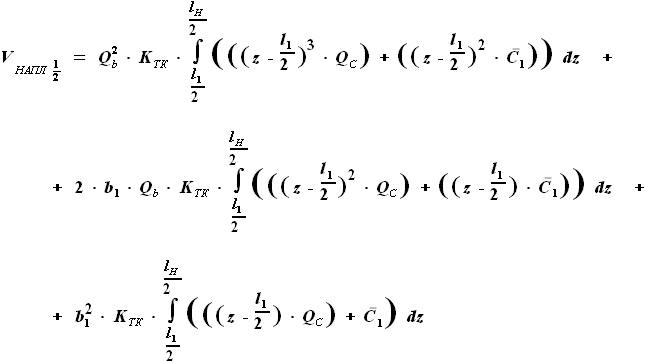
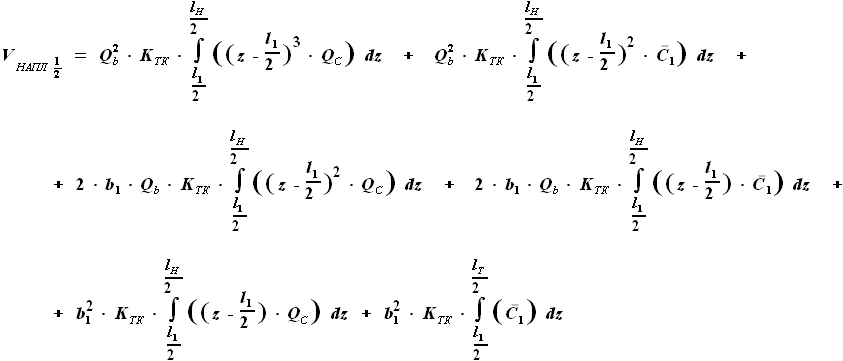
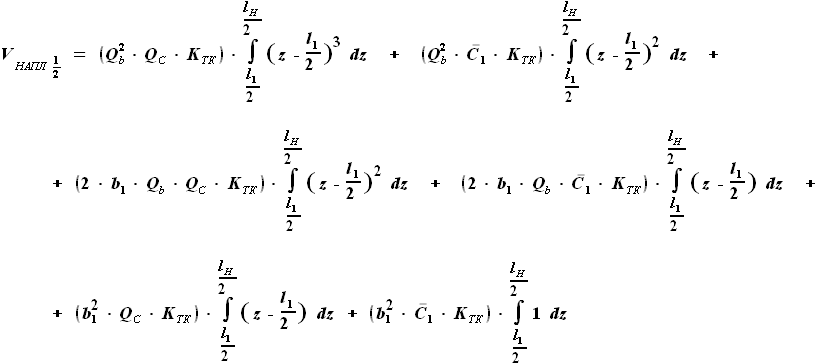
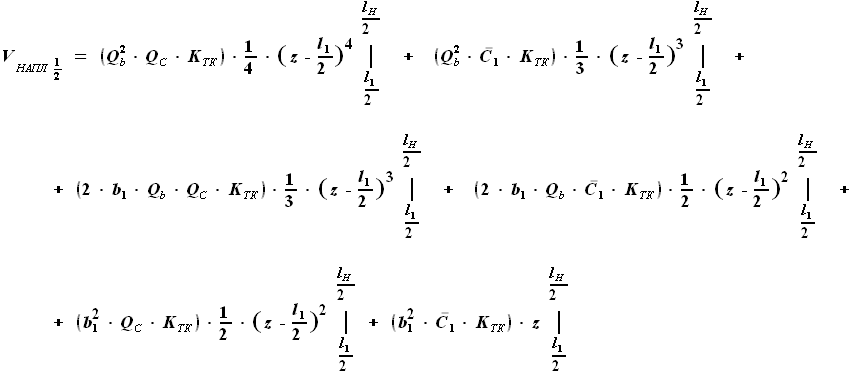
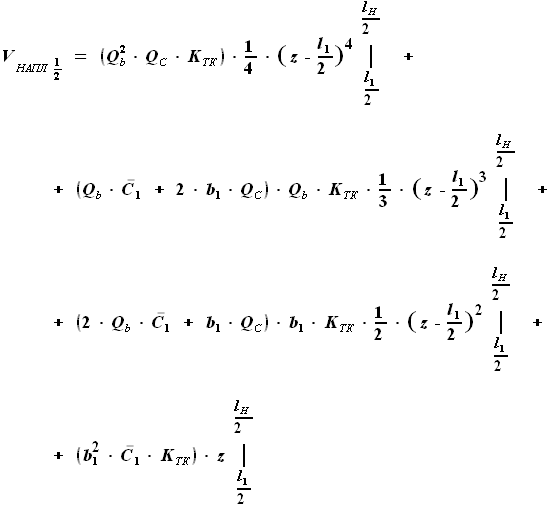
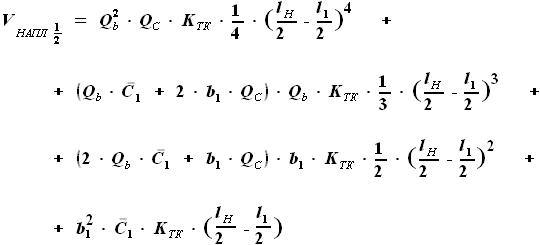
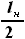 , а конечной границей - координата окончания топливного бака
, а конечной границей - координата окончания топливного бака 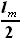 .
.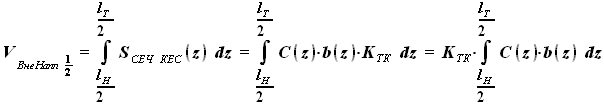 ,
, 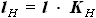 ,
,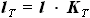 ,
,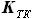 и
и 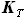 - выбираемые нами параметры, а
- выбираемые нами параметры, а 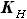 - задан в условии. Для функций b(z) и C(z) выражения были найдены ранее:
- задан в условии. Для функций b(z) и C(z) выражения были найдены ранее: 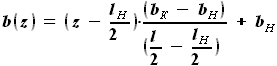
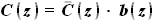 ,
,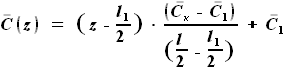
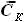 и
и 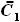 - параметры, заданные в условии.
- параметры, заданные в условии.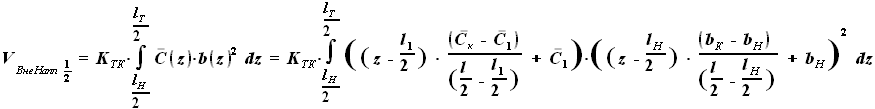
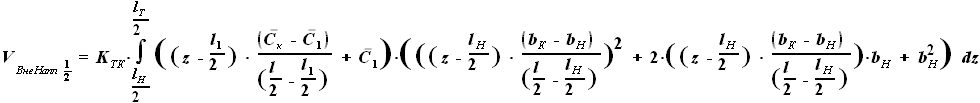
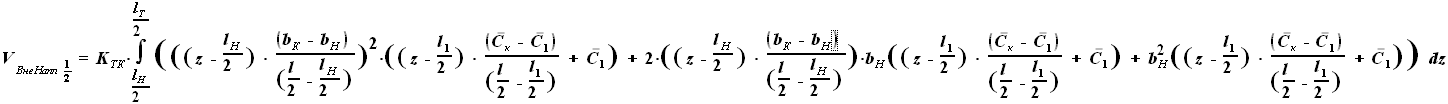
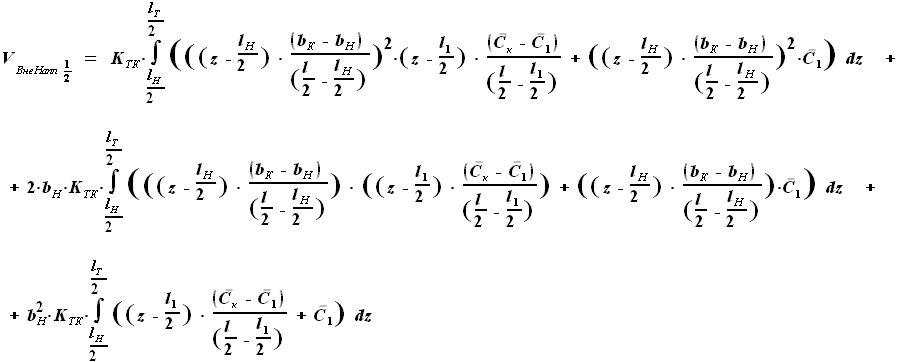
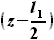 , но и
, но и 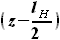 .
Произведение этих сомножителей не является простым увеличением степени.
Чтобы дальнейшие преобразования были аналогичны тем, что проводились
для других участков крыла, представим
.
Произведение этих сомножителей не является простым увеличением степени.
Чтобы дальнейшие преобразования были аналогичны тем, что проводились
для других участков крыла, представим 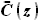 в виде функции, включающей
в виде функции, включающей 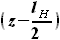 вместо
вместо 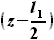 .
.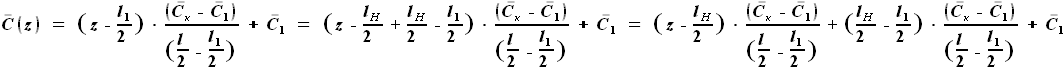
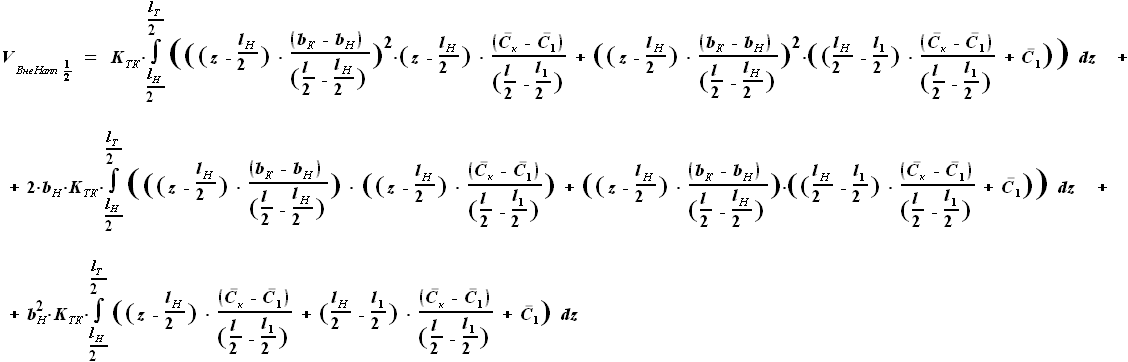
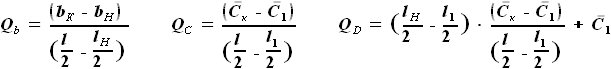
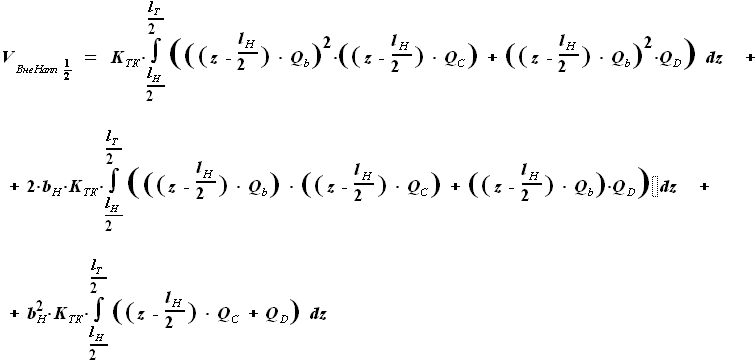
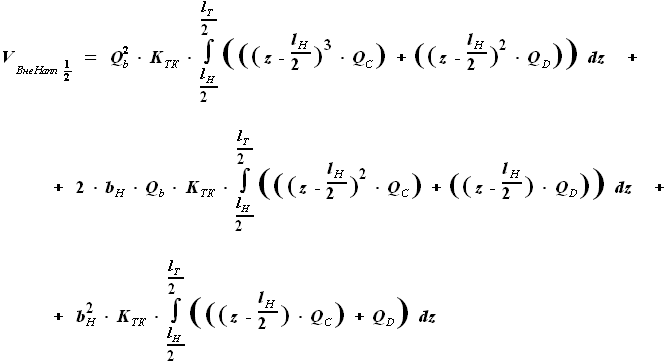
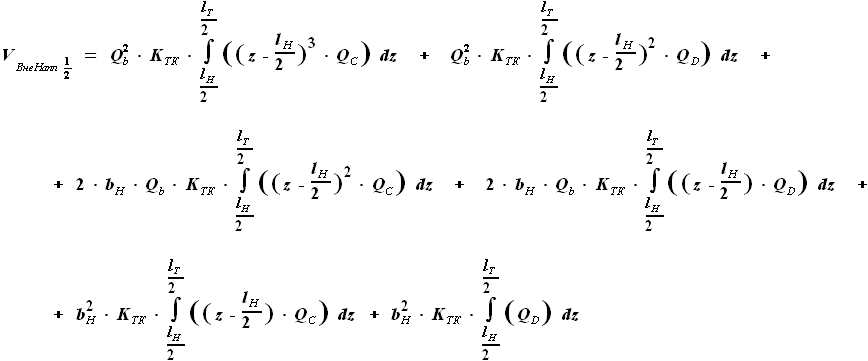
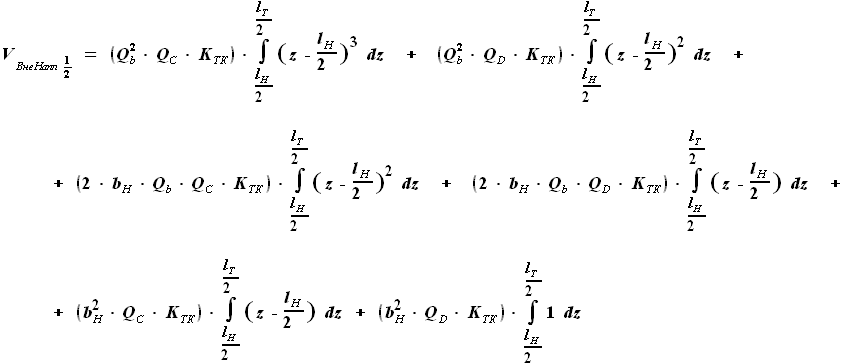
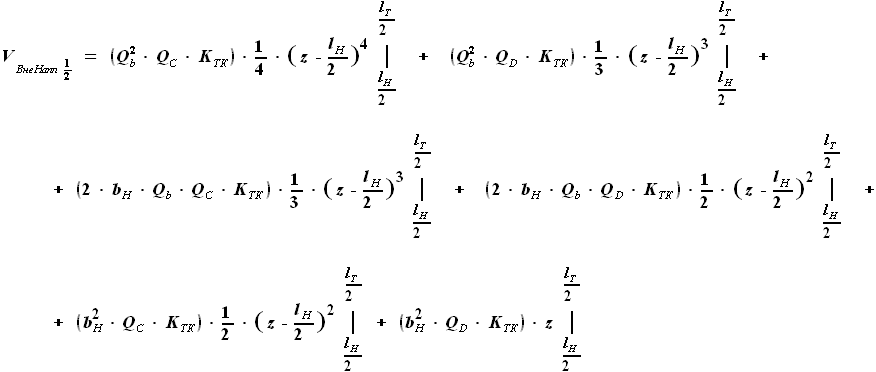
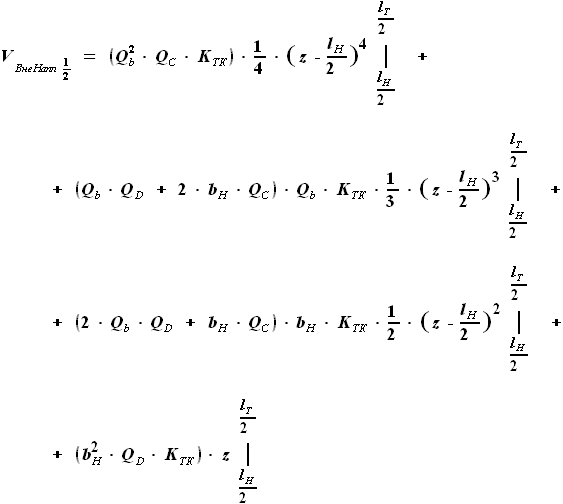
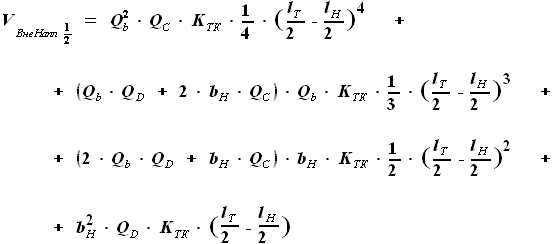
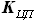 ,
, 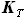 и
и 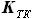 (значение для ещё одного параметра
(значение для ещё одного параметра 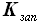 мы уже условились установить на величине 0.75 для военных самолётов и 0.85 для гражданских).
Значения параметров будем выбирать ориентируясь на самолёты-аналоги.
Данные по самолётам-аналогам определяются по имеющимся в открытом
доступе описаниям, таблицам и, особенно, чертежам. Источников,
позволяющих найти значения
мы уже условились установить на величине 0.75 для военных самолётов и 0.85 для гражданских).
Значения параметров будем выбирать ориентируясь на самолёты-аналоги.
Данные по самолётам-аналогам определяются по имеющимся в открытом
доступе описаниям, таблицам и, особенно, чертежам. Источников,
позволяющих найти значения 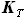 и
и 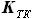 относительно мало, соответственно, при их вычислении выборка по
самолётам-аналогам будет значительно меньше, чем при определении
относительно мало, соответственно, при их вычислении выборка по
самолётам-аналогам будет значительно меньше, чем при определении 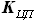 .
.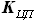 - отношение размаха центроплана к размаху всего крыла:
- отношение размаха центроплана к размаху всего крыла: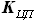 ,
скорее всего, будут свои для каждого класса ЛА.Учитывая это, найдём
величины коэффициента отдельно для каждой группы самолётов-аналогов.
Кроме того, в группе реактивных пассажирских лайнеров выделим для
нахождения
,
скорее всего, будут свои для каждого класса ЛА.Учитывая это, найдём
величины коэффициента отдельно для каждой группы самолётов-аналогов.
Кроме того, в группе реактивных пассажирских лайнеров выделим для
нахождения 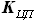 две подгруппы - узко- и широкофюзеляжных самолётов.
две подгруппы - узко- и широкофюзеляжных самолётов.| Стреловидность по передней кромке (град.) | Относительная толщина сечения крыла (%) | Удлинение крыла |
Сужение крыла |
Отношение размаха центроплана к размаху крыла | ||||
| осн. части | наплыва | макс. | мин. | Общее | Части с налывом | |||
| χ | χн | Ĉ max | Ĉ min | λ | η | ηн | Kцп | |
| Параметры, заданные в условии | ||||||||
| вариант 1 (без наплыва) | 32,0 | - | 15,0 | 10,0 | 8,5 | 4,0 | - | - |
| вариант 2 (с наплывом) | 32,0 | 37,0 | 15,0 | 10,0 | 8,5 | 4,0 | 1,7 | - |
| Административные самолёты | ||||||||
| Dassault Falcon 200 | 32,4 | - | н.д. | н.д. | 6,4 | 3,0 | - | 0,128 |
| Dassault Falcon 20E | 33,1 | - | 10,0 | 8,0 | 6,4 | 2,8 | - | 0,129 |
| Dassault Falcon 50 | 26,9 | 35,2 | н.д. | н.д. | 7,5 | 4,0 | 1,9 | 0,110 |
| Challenger 605 | 27,4 | 35,8 | 14,0 | 10,0 | 7,0 | 3,6 | 2,0 | 0,142 |
| Gulfstream G650 | 37,7 | 42,0 | н.д. | н.д. | 7,1 | 5,6 | 1,5 | 0,097 |
| Пассажирские самолёты, узкофюзеляжные | ||||||||
| McDonnel Douglas MD-82 | 28,4 | - | н.д. | н.д. | 8,6 | 5,9 | - | 0,104 |
| Dassault Mercury 100 | 27,8 | 35,5 | н.д. | н.д. | 7,3 | 3,6 | 1,7 | 0,128 |
| Ту-154М | 36,9 | 39,9 | н.д. | н.д. | 7,0 | 5,2 | 2,1 | 0,103 |
| Ил-62М | 38,2 | - | н.д. | н.д. | 6,6 | 4,6 | - | 0,096 |
| Boeing 737-300 | 28,7 | 37,3 | н.д. | н.д. | 7,8 | 5,2 | 1,8 | 0,131 |
| Boeing 737-700 | 25,3 | 40,0 | н.д. | н.д. | 8,6 | 6,0 | 1,6 | 0,111 |
| Airbus A320 | 27,3 | - | н.д. | н.д. | 9,1 | 4,8 | - | 0,118 |
| Boeing 757-200 | 28,0 | - | н.д. | н.д. | 7,3 | 4,5 | - | 0,099 |
| Ту-204 | 30,7 | - | н.д. | н.д. | 8,6 | 4,3 | - | 0,095 |
| Ан-148-100 | 27,6 | - | н.д. | н.д. | 9,5 | 4,0 | - | 0,111 |
| Пассажирские самолёты, широкофюзеляжные | ||||||||
| McDonnel Douglas DC-10 | 38,1 | - | н.д. | н.д. | 6,8 | 4,8 | - | 0,120 |
| Boeing 747-100 | 42,2 | - | н.д. | н.д. | 6,2 | 4,0 | - | 0,108 |
| Airbus A330-200 | 31,5 | - | н.д. | н.д. | 9,5 | 4,8 | - | 0,098 |
| Airbus A340-500 | 31,9 | - | н.д. | н.д. | 9,4 | 4,7 | - | 0,091 |
| Boeing 767-200 | 33,4 | - | н.д. | н.д. | 6,7 | 4,6 | - | 0,118 |
| Boeing 777-200ER | 33,7 | - | н.д. | н.д. | 7,8 | 7,3 | - | 0,103 |
| Boeing 787-800 | 35,3 | - | н.д. | н.д. | 8,0 | 6,6 | - | 0,104 |
| Lockheed L-1011-500 | 37,9 | - | н.д. | н.д. | 7,0 | 5,5 | - | 0,126 |
| McDonnel Douglas MD-11 | 39,0 | - | н.д. | н.д. | 6,4 | 4,1 | - | 0,119 |
| Ильюшин Ил-96-300 | 32,3 | - | н.д. | н.д. | 8,5 | 4,4 | - | 0,105 |
| Ильюшин Ил-86 | 38,1 | - | н.д. | н.д. | 6,4 | 4,4 | - | 0,127 |
| Грузовые самолёты | ||||||||
| Антонов Ан-70 |
16,7 | - | н.д. | н.д. | 9,3 | 3,1 | - | 0,119 |
| Lockheed C-141B | 28,2 | - | 13,0 | 10,0 | 7,9 | 3,1 | - | 0,080 |
| Lockheed C-5B | 27,0 | 29,7 | 12,0 | 11,0 | 7,7 | 2,9 | 1,7 | 0,081 |
| Ильюшин Ил-76МД | 28,2 | - | н.д. | н.д. | 7,9 | 3,7 | - | 0,092 |
| Антонов Ан-124 |
29,1 | 32,9 | н.д. | н.д. | 8,4 | 4,1 | 1,6 | 0,083 |
| McDonnell Douglas C-17A |
28,9 | - | н.д. | н.д. | 7,2 | 4,0 | - | 0,125 |
| British Aerospace BAe.146 |
16,9 | - | н.д. | н.д. | 10,0 | 2,9 | - | 0,114 |
| Антонов Ан-72 |
17,1 | 18,9 | н.д. | н.д. | 9,3 | 3,8 | 2,3 | 0,081 |
| Kawasaki C-1 |
24,8 | 29,3 | н.д. | н.д. | 7,4 | 3,6 | 1,6 | 0,116 |
| Бомбардировщики | ||||||||
| Sud Aviation Vautour II | 37,5 | - | н.д. | н.д. | 5,1 | 2,1 | - | 0,091 |
| Алексеев Самолёт 150 | 37,8 | - | 11,8 | 11,0 | 4,8 | 1,9 | - | 0,106 |
| Douglas A-3 Skywarrior | 38,5 | - | ? | ? | 6,8 | 2,9 | - | 0,099 |
| Boeing B-47E Stratojet | 36,2 | - | ? | ? | 9,4 | 2,4 | - | 0,079 |
| Ильюшин Ил-30 | 35,8 | - | 12,0 | 12,0 | 5,8 | 2,3 | - | 0,063 |
| Ильюшин Ил-46 | 37,5 | - | н.д. | н.д. | 7,1 | 3,0 | - | 0,072 |
| Туполев Ту-16 | 36,8 | 42,6 | 15,7 | 12,0 | 6,2 | 2,5 | 1,6 | 0,058 |
| Vickers Valiant B.1 | 25,2 | 44,4 | н.д. | н.д. | 5,6 | 4,1 | 1,8 | 0,094 |
| Boeing B-52H | 37,8 | - | н.д. | н.д. | 8,6 | 2,8 | - | 0,062 |
| Мясищев 3МД | 36,9 | 40,7 | н.д. | н.д. | 7,7 | 4,8 | 2,0 | 0,073 |
| группа ЛА | Значение параметра Kцп (отношение размаха центроплана к размаху крыла) | |
| среднее по аналогам | выбранное | |
| Административные самолёты | 0,1211352319 | 0,125 |
| Пассажирские самолёты, узкофюзеляжные | 0,1094797105 | 0,11 |
| Пассажирские самолёты, широкофюзеляжные | 0,1108253241 | 0,111 |
| Грузовые самолёты | 0,0990795364 | 0,099 |
| Бомбардировщики | 0,0797639302 | 0,08 |
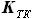 - отношение площади сечения кессона к площади прямоугольника b x C, в который вписано сечение крыла:
- отношение площади сечения кессона к площади прямоугольника b x C, в который вписано сечение крыла: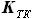 по конкретным самолётам, встречается в открытом доступе довольно
редко. Поэтому мы будем вынуждены ограничиться одним общим
результирующим значением коэффициента, взятым как среднее по всем
самолётам, для которых удалось найти информацию.
по конкретным самолётам, встречается в открытом доступе довольно
редко. Поэтому мы будем вынуждены ограничиться одним общим
результирующим значением коэффициента, взятым как среднее по всем
самолётам, для которых удалось найти информацию.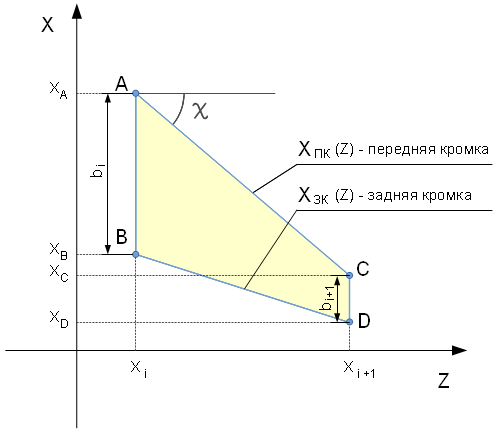
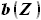 будет равна расстоянию между передней и задней кромками, то есть, разности функций
будет равна расстоянию между передней и задней кромками, то есть, разности функций 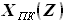 и
и 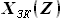 ,
,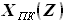 - функция, описывающая положение передней кромки крыла на участке от
- функция, описывающая положение передней кромки крыла на участке от 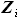 до
до 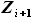
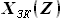 - функция, описывающая положение задней кромки крыла на участке от
- функция, описывающая положение задней кромки крыла на участке от 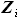 до
до 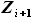
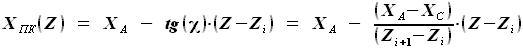
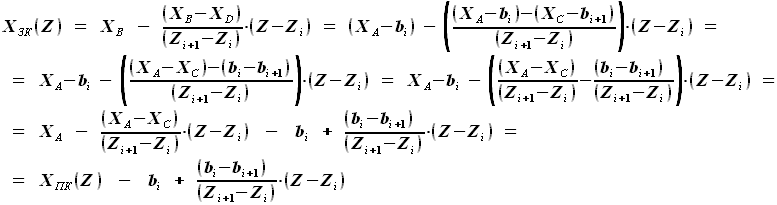
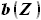 на участке от
на участке от 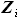 до
до 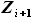 будет равна
будет равна 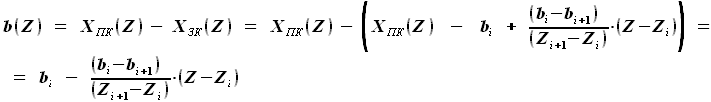
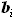 и
и 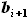 и расстояния между ними
и расстояния между ними 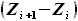 .
Координаты
.
Координаты 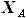 и
и 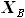 (и выражаемые через них
(и выражаемые через них 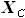 и
и 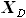 ) не входят в
) не входят в 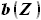 , то есть, имеют значение только расстояния между точками A, B, C и
D, а не их абсолютные координаты на плоскости XZ (что, в общем-то,
очевидно). Отметим также, что в выражении
, то есть, имеют значение только расстояния между точками A, B, C и
D, а не их абсолютные координаты на плоскости XZ (что, в общем-то,
очевидно). Отметим также, что в выражении 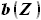 присутствуют разность
координат по оси X между A и B (это
присутствуют разность
координат по оси X между A и B (это 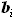 ) и между C и D (это
) и между C и D (это 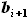 ), а
расстояние по X между точками A и C, как и равное ему расстояние между
B и D, - отсутствуют. А так как именно разность
), а
расстояние по X между точками A и C, как и равное ему расстояние между
B и D, - отсутствуют. А так как именно разность 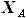 и
и 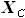 определяет
стреловидность фрагмента крыла при его фиксированном размахе
определяет
стреловидность фрагмента крыла при его фиксированном размахе 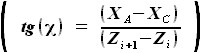 , то получается, что длина местной хорды
, то получается, что длина местной хорды 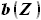 не зависит от угла стреловидности.
не зависит от угла стреловидности.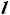 ),
корневая и концевая хорды (
),
корневая и концевая хорды (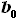 и
и 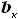 ), а для крыла с наплывом - также
хорда, соответствующая концу наплыва (
), а для крыла с наплывом - также
хорда, соответствующая концу наплыва (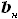 ).
).